如何在Geogebra中绘制分段函数图像

在数学中制作试卷、课件中经常用到分段函数图象或者函数在某一区间内的图象问题，“如果”指令能轻易地实现这一效果。在GeoGebra中基本形式为：

1
如果(条件, 成立时返回的值, 不成立时返回的值)

这个函数会根据条件的真假来返回对应的值。提前说一句，这里的如果，就是判断语句if，使用的地址，就是Geogebra的输入栏，有些朋友的输入指令框不能输入中文，也就是输入中文之后不显示内容，暂时不知道什么问题，日后更新。

1.基础函数

绘制函数在指定区间内的图象：指令格式：

1
如果[ <条件>, <结果> ]

指令范例：

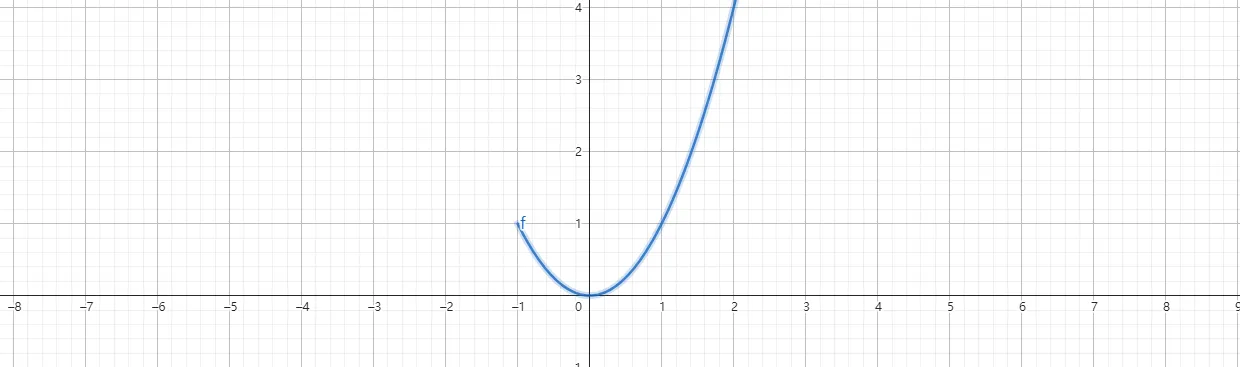
1
如果[-1<=x<=3,x^2]

指令功能：作出函数y=x²,x∈[-1,3]的图象。图像如下图

2.两段函数

绘制多分段函数的图象： 指令格式：

1
如果[ <条件>, <结果>, <否则> ]

指令范例：

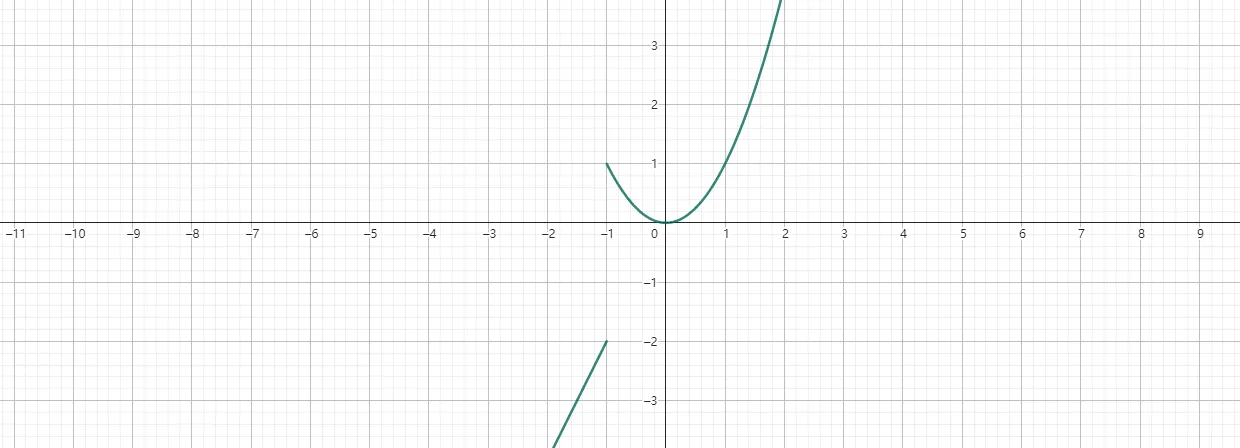
1
如果[x<=-1,2x,x^2]

指令功能：作出对应分段函数的图象，在x<=-1的区间之内，显示y=2x的图像，在x>-1的区间之内，显示y=x²图像

3.多段函数

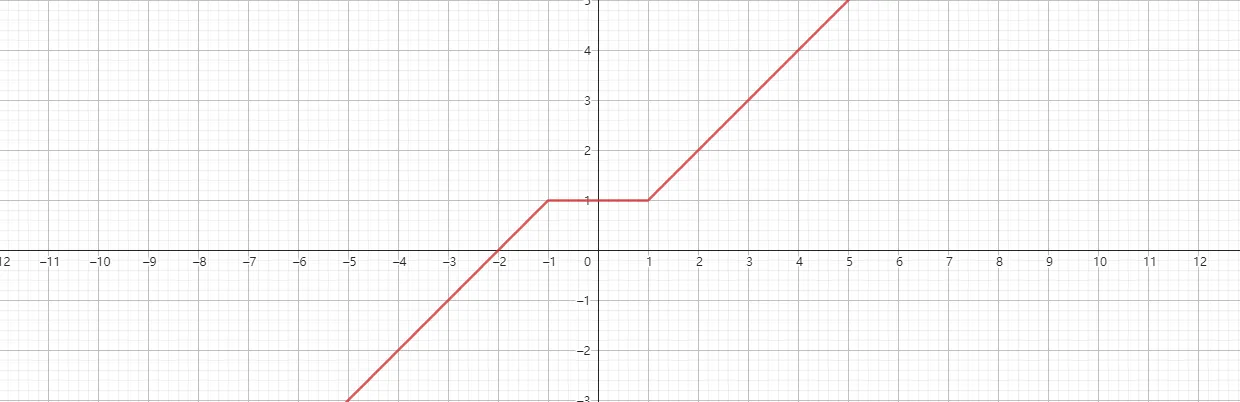
若要绘制两段以上的分段函数，也需要在“如果”指令中嵌套一层“如果”指令，比如绘制如下的图像，

指令为：

1
如果[x<-1, x+2, 如果[x<=1,1,x]]

或者是

1
如果[x<=1, 如果[x<-1,x+2,1],x]

这段函数分为三部分，第一部分是自变量在x<-1区间内，画出函数y=x+2的图像，在-1<x<1的区间内，画出y=1的图像，余下也就是x>1的区间，画出y=x的图像。不太理解第二个指令的运行逻辑，但是并不影响他的正确性。

在 GeoGebra 中显函数可通过 if( ) 命令限制函数的取值范围，比如在指令框输入如下指令代码

1
f(x) = if(x>0 , x^2)

会得到如下图像

4.隐式方程

而对于隐式方程，GeoGebra 官方文档中却并没有提供方法。通常我们处理的方法有以下三种。

4.1利用布尔值限制取值范围

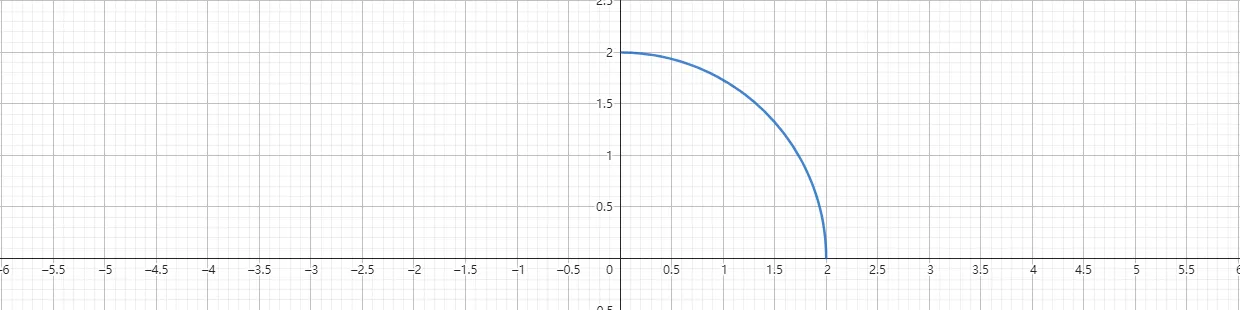
一个通用的方法是，将方程整理为f(x,y)=0的形式，再将右边除以一个布尔值，因为分母不能为零，所以只有布尔值返回为1 的时候（条件为真），方程有意义才会输出结果。比如我们想要画出圆x²+y²=4在x>0且y>0区域的图像，可以将方程写成如下形式。逻辑运算符可以用 && 代替。

1
x^2 + y^2 -4 =0/(x>0&&y>0)

在这里简单说一下Geogebra的逻辑运算符：

  1. 逻辑与（AND）

    符号：∧（需通过辅助键盘输入）或 &&（快捷键）

    用途：用于多个条件同时成立的情况，如判断点是否在圆内时结合半径条件3。

  2. 逻辑或（OR）

    符号：∨（需通过辅助键盘输入）或 ||（快捷键）

    用途：用于多个条件中任一成立即可触发效果，如判断线段是否与圆相交3。

  3. 逻辑非（NOT）

    符号：¬（需通过辅助键盘输入）或 !（快捷键）

    用途：用于反转条件判断，如隐藏不符合条件的图形。

当然，还可以把方程写成如下形式也可以起到同样效果。

1
x^2 + y^2 - 4 + lg(x) - lg(x) + lg(y) -lg(y) = 0

4.2将一般方程转化为参数方程

比如圆x²+y²=4的参数方程为

$$
\left{\begin{array}{l} x=2 \cos \theta \ y=2 \sin \theta \end{array}\right. \
$$
如果想要画出同样的效果，还可以使用 curve( ) 曲线命令画出参数曲线

Curve( , , , , )
曲线( <表达式>, <表达式>, <参变量t>, <起始值>, <终止值> )

1
curve( 2cos(θ) , 2sin(θ) , θ , 0 , π/2 )

都可以得到上图的图像。

4.3轨迹法

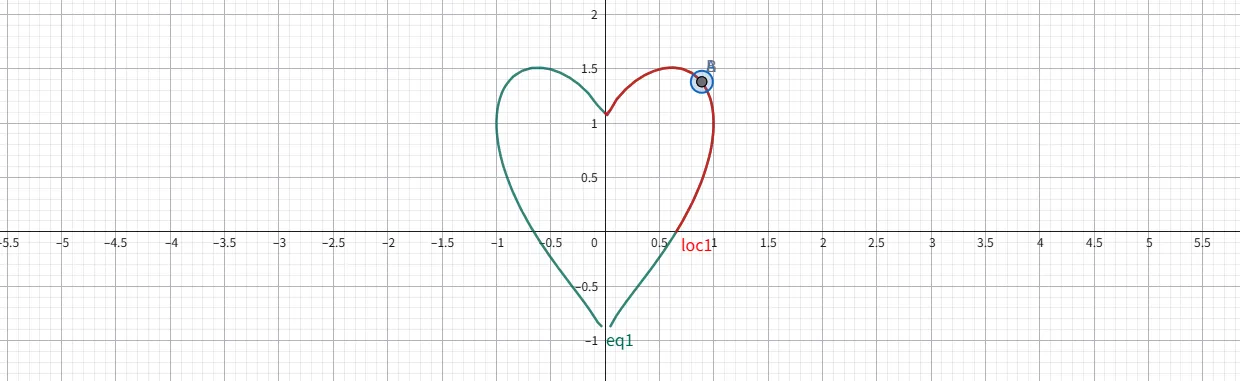
利用 locus( ) 命令绘制红色区域内的曲线。利用 locus( ) 轨迹命令绘制要比方法一效果好得多，比方法二在数学处理上简单得多，步骤如下。绘制隐式曲线，并在曲线上取任意一点

1
x^2+(y-cbrt(x^2))^2=1

直接在命令栏输入以上命令的话，默认名称为eq1

1
A = point( eq1 )

创建一个点，当曲线上的点（ 点）在取值范围内时，将曲线上的点赋值给新创建的点。

1
# x( ) 函数用于获得点的横坐标，y( ) 同理
1
xmin=0
1
xmax=1
1
ymin=0
1
ymax=2
1
B = If(xmin ≤ x(A) ≤ xmax ∧ ymin ≤ y(A) ≤ ymax, A)

其中插入最后一行代码的时候，如果点A不在设定的区间之内，会出现异常，但是不是错误，只需要用鼠标调整点A的位置就可以。然后我们利用locus( ) 命令来绘制轨迹图像。

Locus( , )
轨迹( <构造轨迹线的点>, <点> )

locus( ) 命令中第二个参数必须是对象上的点，第一个参数是从属于第二个参数的点，比如上面的命令中点 就是依赖于点 创建的，locus( ) 命令会返回第一个参数点的轨迹。

1
Locus(B, A)

在绘制隐式方程的曲线时，能够用方法二的情况下优先选方法二，其次是方法三，方法一简单但代码运行很低效（卡顿、曲线显示不全），值得注意的是，方法一与方法三创建的对象都是路径，这意味着作用于路径对象上的命令只有 point( ) 能被使用。